Для решения многих геометрических задач, связанных с тетраэдром и параллелепипедом, полезно научиться и уметь строить на рисунке их сечения различными плоскостями. 

В этом поможет данный сценарий, в котором наглядно с расположением в пространстве всех элементов, продемонстрированно построение сечения и проекцию которого можно закрепить в виде рисунка на доске.

Уточним, что понимается под сечением тетраэдра или параллелепипеда. Назовем секущей плоскостью тетраэдра (параллелепипеда) любую плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллелепипеда). Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра (параллелепипеда). Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырехугольники. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.

При построении сечений параллелепипеда на рисунке следует учитывать тот факт, что если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны (свойство).
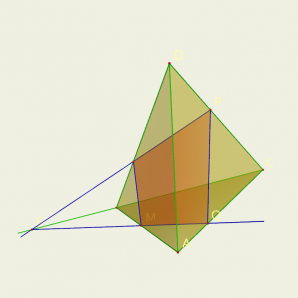
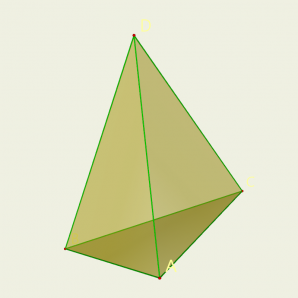
Сценарий: Рассмотрим пример построения сечения тетраэдра.

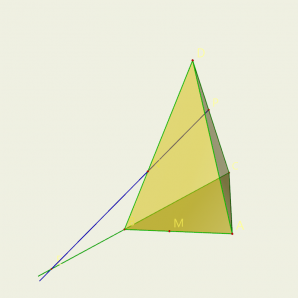
В пространстве появляется тетраэдр. Его можно вращать в 3-х плоскостях. На ребрах АВ, BD и CD тетраэдра ABCD отмечаются точки М, N и Р. Задача: Построить сечение тетраэдра плоскостью MNP.

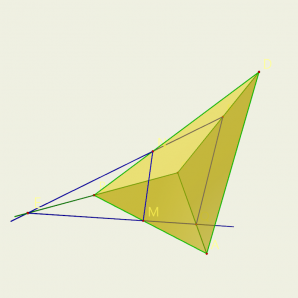
Под управлением, появляются на гранях прямые, по которым плоскость MNP пересекается с плоскостью грани ABC. Точка М является общей точкой этих плоскостей. Для построения еще одной общей точки продолжаются отрезки NP и ВС до их пересечения в точке Е, которая и будет второй общей точкой плоскостей MNP и ABC. Следовательно, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро АС в некоторой точке Q. Четырехугольник MNPQ — искомое сечение.

Получившуюся модель с элементами построения можно вращать в 3-х плоскостях и менять масштаб.